こんにちは、lizard.kです。
昨日の日経ヴェリタスで金融広報中央委員会が発表した金融リテラシークイズについて触れている記事がありました。クイズの内容は以下のサイトで見ることが出来ます(たった5問ですので興味のある方は是非解いてみてください)。
この中で、「10万円の借入れがあり、借入金利は複利で年率20%です。返済をしないと、この金利では、何年で残高は倍になるでしょうか。」という問題があります。
これは「72の法則」が使えるかどうかを試す問題です。ご存知の方も多いと思いますが、「72の法則」とは72を年利で割れば何年で2倍になるか分かるという便利な計算式のことです。
先程の例では、72÷20=3.6なので、約3年半で2倍になることが分かります。
これを使えば、前回「老後2,000万円不足問題」に関して書いた記事の中の、5%で運用した場合も
72÷5=14.4 だから、約14年半で資産が倍になるなんてのがパッと分かるわけです。6%なら72÷6=12だから12年で倍、7%なら約10年で倍とすぐ分かります。便利ですよね!
ただ、この法則は知っていても「何で72なのか」を考えたことはありませんでした。調べてみると以下のような解説が見つかりました。
元金を X (> 0)、年利率を r (> 0) とし、n 年後に元利合計が2倍になるとすれば、
$$X(1+r)^n=2X$$
となる。この両辺の自然対数をとると$$n\log(1+r)=\log2$$
$$n=\frac{\log2}{\log(1+r)}$$
ここで、r ≪ 1、すなわち r が 1 に比べて十分に小さい場合には、log(1 + r) ≒ r と近似できるので、$$n\approx\frac{\log2}{r}\approx\frac{0.693}{r}$$
となる。すなわち「倍増年」は、「0.693を年利で割った値」又は「69.3を年利(%表示)で割った値」で近似できる。実用上は、69.3を切りの良い70や約数の多い72で置き換えることが多い。
なるほど69.3に近くて約数が多いから72ってことなんですね。
ほとんどは高校レベルの数学で理解できる説明ですが、一箇所引っかかるのが、「r が 1 に比べて十分に小さい場合には、log(1 + r) ≒ r と近似できる」という部分です。
最初に読んだ時は、rが1に比べて十分に小さいということは、log(1 + r)≒log 1≒0 ってこと???とか考えてました。それだとnを求める際にrで割れませんが、、、
これはマクローリン展開という奴で、
$$\log(1+r)=r-\frac{r^2}{2}+\frac{r^3}{3}-…$$
と書けるから、r が 1 に比べて十分に小さい場合には log(1 + r) ≒ r と近似できるってことのようです。
そういえば、テイラー展開とかマクローリン展開は大学のときにやりましたよ!当時はちんぷんかんぷんだったけど、こんなところで役に立つとはなー。数学って大事!
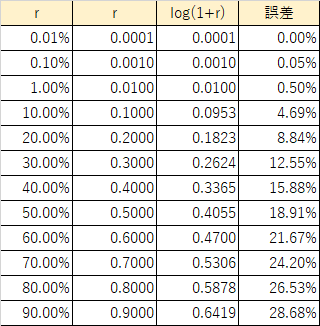
実際にExcelのLN関数で色々と数字を変えて試してみましたが、金融リテラシークイズに出ていた20%なんかは1に比べて十分に小さいと言えるか微妙なところで誤差も結構あることが分かりますね。
というわけで、錆びついた頭を久しぶりに使いました(笑)が、ちょっと楽しかったので、以下の本でも読んで復習してみようかと思っているところです。

WordPressで数式を書くためにMathJax-LaTeXを入れてみました。TeXで書くのも久しぶりだけど、便利だなこれ。



コメント